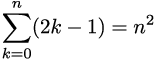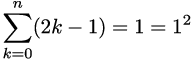Few years ago I found an interesting pattern, playing with some programming algorithm. I am not sure if I defined the pattern well in terms of math language, despite I was trying to be as close as possible. The hypothesis is:
A sum of all members of consecutive natural odd numbers set equals to amount of set members squared.
Hence,
| Set | Amount of set members | Sum of set members | Formula |
| 1 | 1 | 1 | 1 = 1 ^ 1 |
| 1,3 | 2 | 4 | 1 + 3 = 2 ^ 2 |
| 1,3,5 | 3 | 9 | 1 + 3 + 5 = 3 ^ 2 |
| 1,3,5,7 | 4 | 16 | 1 + 3 + 5 + 7 = 4 ^ 2 |
| 1,3,5,7,9 | 5 | 25 | 1 + 3 + 5 + 7 + 9 = 5 ^ 2 |
Let’s prove the pattern works for any set by mathematical induction.
Proof
For n = 1 is true:
Suppose that:
We need to show that:
Indeed,
What proves the Hypothesis. I am totally sure the thing proven is something simple and very fundamental, but I still hope, I’m the first who discovered it:) I also hope there is practical application for it. Unfortunately, I’m mathematically ignorant and I have no clue on what the above means.